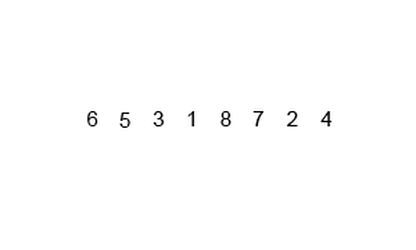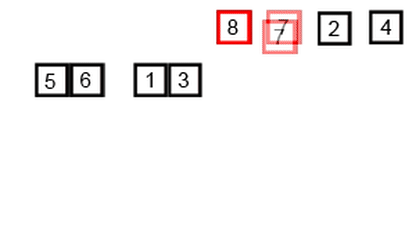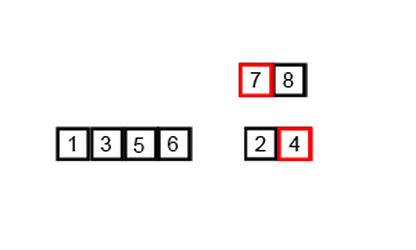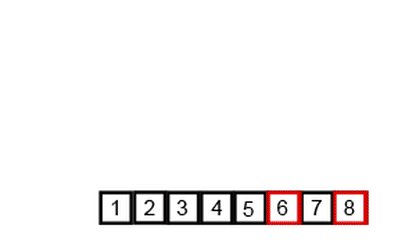
🔎퀵 정렬은 재귀 함수 및 분할 정복 개념이 들어 있음
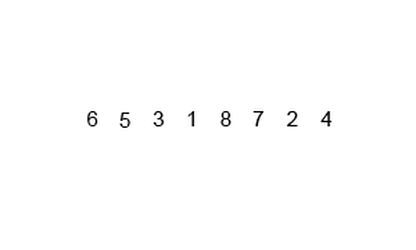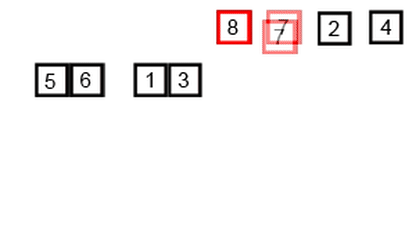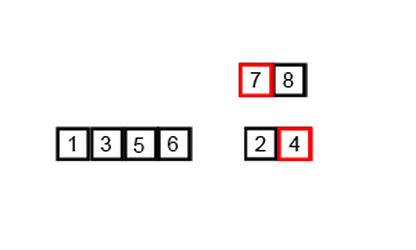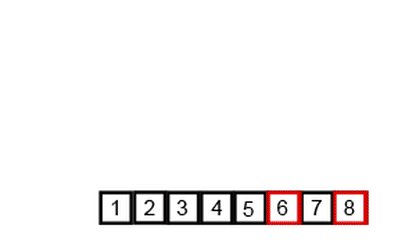
#include <stdio.h>
int number = 8;
int sorted[8]; //정렬 배열은 반드시 전역 변수로 선언
void merge(int a[], int m, int middle, int n){
int i = m;
int j = middle+1;
int k = m;
//작은 순더대로 배열에 삽입
while(i <=middle && j <= n){
if(a[i]<a[j]){
sorted[k]=a[i];
i++;
}
else{
sorted[k]=a[j];
j++;
}
k++;
}
// 남은 데이터도 삽입
if(i > middle){
for(int t = j; t <= n; t++){
sorted[k]=a[t];
k++;
}
}
else{
for(int t = i; t <= middle; t++){
sorted[k] = a[t];
k++;
}
}
//정렬 된 배열을 삽입
for(int t = m; t<=n; t++){
a[t]=sorted[t];
}
}
void mergeSort(int a[],int m, int n){
if(m < n){ //무한으로 안들어가게 해줌 ex) mergeSort(a, 2, 2) 들어오면 계속 2, 2로 들어감
int middle = (m+n)/2;
mergeSort(a, m, middle);
mergeSort(a, middle+1, n);
merge(a, m, middle, n);
}
}
int main(){
int array[number] = {10, 9, 8, 7, 6, 5, 4, 3};
mergeSort(array,0,number-1);
for(int i=0; i<number; i++){
printf("%d ", array[i]);
}
}
Time complexity 가 n*logN 인 이유는 O(n) 이 merge를 할때의 시간복잡도이며, O(logn) 이 binary search (divide) 할때의 시간복잡도 이기에 한번의 iteration 에서 O(nlogn)이 시간복잡도가 완성된다.
🔎 단, 추가적인 데이터 저장공간 이용 메모리 측면에서 비효율적일 수 있음