설명:

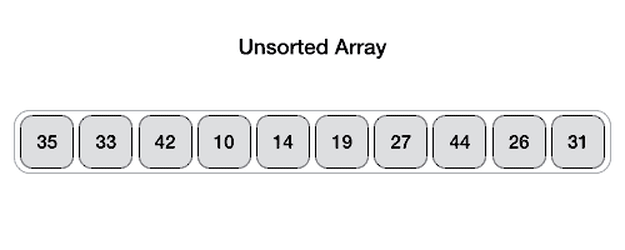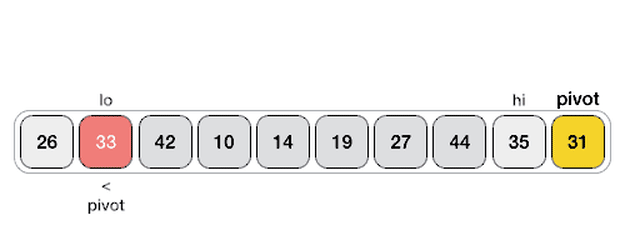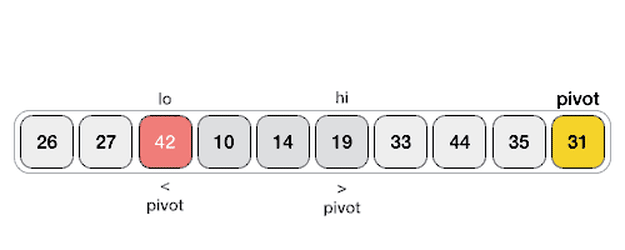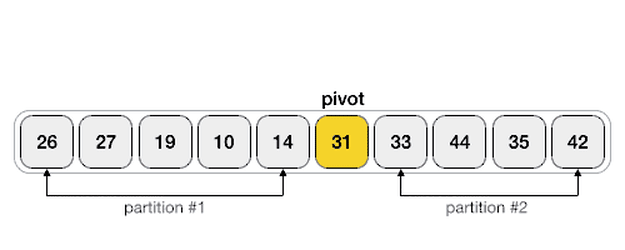
🔎퀵 정렬은 재귀 함수 및 분할 정복 개념이 들어 있음

1. Pivot 값을 정하고 pivot 보다 큰 숫자를 나머지 array에서 왼쪽부터 찾고 작은 수를 오른쪽부터 찾음
2. 찾았을 경우 왼쪽 값과 오른쪽 값을 바꿈
3. 1번과 2번을 계속 반복 하는데 왼쪽 값이 오른쪽으로 계속 가고 오른쪽 값이 계속 왼쪽으로 가다가 두 숫자가 엇갈릴 경우 오른쪽에서부터 내려와서 만난 첫번째 작은 값과 pivot 값의 위치를 바꿔주면 된다.
4. 그러면 바뀐 pivot을 기준으로 왼쪽은 pivot보다 작아지고 오른쪽은 pivot보다 큰 숫자가 남는데 남은 왼쪽 오른쪽 부분을 1, 2, 3번 과정과 똑같이 재귀함수를 이용하여 분할 정복 해주면 된다.

예시:

예시 코드:

#include <iostream>
using namespace std;

int number = 10;
int data[10]={5, 9, 8, 7, 6, 10, 4, 3, 2, 1};

void quickSort(int *data, int start, int end){
	if(start >= end){ //원소가 1개인 경우 
		return;
	}
	int key = start; //키는 첫번째 원소 
	int i = start + 1;
	int j = end; 
	int temp;
	
	while(i <= j){ // 엇갈리 때가지 반복
		while(data[i] <= data[key]){  //키 값보다 큰 값을 만날때까지 오른쪽으로 이동 
			i++;	
		}
		while(data[j] >= data[key] && j > start){ //키 값보다  작은 값을 만날때까지 왼쪽으로 이동 
			j--;
		}
		if(i>j){ //현재 엇갈린 상태면 키 값과 교체 
			temp = data[j];
			data[j] = data[key];
			data[key] = temp;
		}
		else {
			temp = data[j];
			data[j] = data[i];
			data[i] = temp;
		}
	}
	
	quickSort(data, start, j-1);
	quickSort(data, j+1, end);
}

int main(){
	quickSort(data, 0, number - 1);
	
	for(int i=0; i<10; i++){
		cout<<data[i]<<" ";
	}
	return 0;
}

시간 복잡도:

Worst case: O(N^2)

평소: O(NlogN)

문제 풀이:

#include <iostream> using namespace std;

int number = 10; int data[10]={5, 9, 8, 7, 6, 10, 4, 3, 2, 1};

void quickSort(int *data, int start, int end){ if(start >= end){ //원소가 1개인 경우 return; } int key = start; //키는 첫번째 원소 int i = start + 1; int j = end; int temp;

while(i <= j){ // 엇갈리 때가지 반복
	while(data[i] <= data[key]){  //키 값보다 큰 값을 만날때까지 오른쪽으로 이동
		i++;
	}
	while(data[j] >= data[key] && j > start){ //키 값보다  작은 값을 만날때까지 왼쪽으로 이동
		j--;
	}
	if(i>j){ //현재 엇갈린 상태면 키 값과 교체
		temp = data[j];
		data[j] = data[key];
		data[key] = temp;
	}
	else {
		temp = data[j];
		data[j] = data[i];
		data[i] = temp;
	}
}

quickSort(data, start, j-1);
quickSort(data, j+1, end);